Theory of Automata Real-world Applications

 

Automata theory has several real-world applications in a variety of domains since it deals with abstract machines and the issues they might resolve. Automata theory is important in the following domains: 

Computer Science and Programming Languages:
Automata play a crucial role in compiler design, particularly in lexical analysis. Token recognition in source code is achieved by using finite automata to implement patterns defined by regular expressions.
Verifying Syntax Pushdown automata and context-free grammars aid in the parsing and comprehension of programming language structure, ensuring that code follows proper syntax.

NLP, or natural language processing,

Text Parsing: To analyze and comprehend human language, finite state machines and probabilistic automata are employed in a variety of natural language processing (NLP) applications, including named entity recognition and part-of-speech tagging.

Speech Recognition: To describe sound sequences, speech recognition systems frequently employ Hidden Markov Models (HMMs), a kind of probabilistic automaton.

Network Protocols:
Protocol Verification: The use of automata theory facilitates the modeling and verification of communication systems and network protocols to make sure they function as intended under various circumstances.

Finite state machines can be used to model and analyze network traffic patterns, which can aid in performance monitoring and security.

Systems of Control:

Automata are utilized in the design of control and embedded systems, including those seen in robotics and automation. Systems states and transitions can be modeled and controlled with the use of finite state machines.

Game Creation:

Behavior Modeling: Character and game element behavior is created and managed using automata models, such as finite state machines, to enable more dynamic and responsive interactions.

The field of bioinformatics

Sequence Analysis: In bioinformatics, automata are utilized for sequence alignment and analysis, including pattern recognition in protein structures or DNA sequences.

Design of Hardware:

Digital Circuit Design: To ensure that digital circuits and controllers function properly under a variety of circumstances, finite state machines are utilized in their design and implementation.

Robotics and Automation:

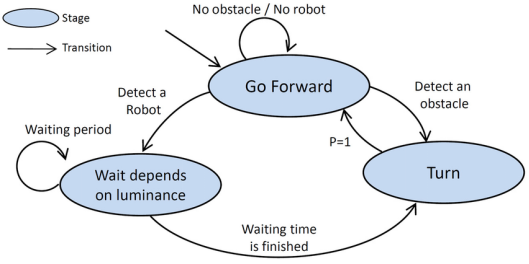
Path Planning: Finite state machines and other automata are used in robotics for path planning and obstacle avoidance. They help robots navigate complex environments by defining states for different stages of movement and decision-making.

Artificial Intelligence:

Behavior Trees: In AI, particularly in game AI, behavior trees use principles from automata theory to manage complex behaviors and decision-making processes in a structured way.

Data Compression:

Algorithm Design: Automata are used in algorithms for data compression. For example, the Lempel-Ziv-Welch (LZW) algorithm, which is used in file compression formats like GIF, relies on concepts from automata theory to efficiently encode data.

Text Search Algorithms:

Pattern Matching: Automata are fundamental to efficient text search algorithms. For instance, the Aho-Corasick algorithm uses a finite state machine to search for multiple patterns simultaneously in a text, making it highly efficient for applications like searching in large databases.

Cryptography:

Random Number Generation: Some cryptographic systems use automata to generate pseudorandom sequences of numbers. Linear feedback shift registers (LFSRs), which are a type of finite state machine, are commonly used in cryptographic applications for secure key generation and random number generation.

Understanding Self-Attention: The Core Mechanism Behind Transformers

Self-attention has become a key mechanism in artificial intelligence nowadays, driving some of the most sophisticated models in natural language processing (NLP) and other fields. Let's examine self-attention's foundations, advantages, and influence on machine learning to see why it is so revolutionary.

What is Self-Attention?

One of the main mechanisms in the Transformer architecture that enables a model to assess the relative relevance of various parts in a sequence is self-attention. Self-attention processes every element simultaneously, as opposed to standard models that process input sequentially. This improves efficiency and accurately reflects long-range dependencies.

 Self-attention is flexible enough to handle a wide range of data formats because it can concentrate on pertinent portions of the input by creating query, key, and value vectors from each token and calculating attention scores. This capacity has transformed domains such as computer vision and natural language processing, propelling progress in models like BERT and GPT.

How Does Attention to Oneself Operate?
In summary, each input token is used to create three vectors—a query vector, a key vector, and a value vector—that are then used by self-attention. Following that, these vectors are utilised to calculate attention scores, which establish the relative emphasis that each token in the sequence should acquire from the other tokens.

Query, Key, and Value Vectors: Using acquired linear transformations, every character in the input sequence is converted into one of these three vectors.

Attention Scores: To determine an attention score, take the dot product of a token's query vector and all of the tokens' key vectors. How much weight a token should provide to other tokens is indicated by this score.

Scaling: The scores are scaled by the square root of the dimension of the key vectors in order to keep the dot product from getting too big, which could compromise the stability of the gradients during training.

Softmax: To normalise the scaled scores into a probability distribution, they are run via a softmax function.

Weighted Sum: The final output representation for each token is obtained by adding the weights assigned to each value vector by these normalised scores.

Understanding the p-Value: A Key Concept in Statistical Hypothesis Testing

 The p-value is a vital notion in statistics that aids researchers in assessing the relevance of their findings. However, what is a p-value exactly, and why is it so significant?

A p-value: what is it?
In a statistical test, the p-value, also known as the probability value, is a metric that indicates how strong the evidence is against the null hypothesis. Generally speaking, the null hypothesis states that there is no impact or difference. In a clinical trial, for instance, the null hypothesis can claim that a novel medication has no effect when compared to a placebo.

How Does One Use the p-Value?
A p-value is computed during a hypothesis test to determine whether the null hypothesis should be rejected or not. This is a streamlined procedure:

• Construct Hypotheses: Describe your alternative hypothesis (H₁) and null hypothesis (H₀).
• Select the Level of Significance (α): The standard options are 0.05 and 0.01.
• Determine the p-Value. Conduct the examination and determine the p-value.
• P-Value in relation to α
• Reject the null hypothesis if the p-value is less than or equal to α.
• Do not reject the null hypothesis if the p-value is greater than α.  

How to Interpret the p-Value

• A low p-value (≤ α) suggests that there is an inconsistency between the observed data and the null hypothesis. This shows that there is a statistically significant influence in your data.
• Elevated p-value (more than α): Indicates that the observed data aligns with the null hypothesis. This indicates that the alternative hypothesis is not well supported by the available data.

Example: t-Test Calculation

Consider a simple example using Python's scipy library to perform a t-test:

from scipy import stats

import numpy as np

data1 = np.array([5, 6, 7, 5, 6])

data2 = np.array([8, 9, 10, 8, 9])

t_stat, p_value = stats.ttest_ind(data1, data2)

print("p-Value:", p_value)