Theory of Automata Real-world Applications

 

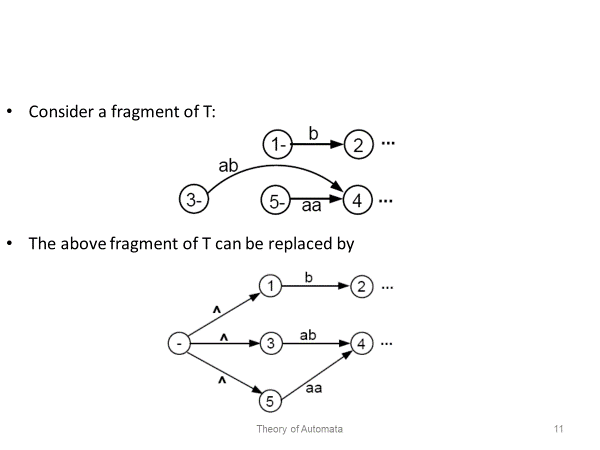
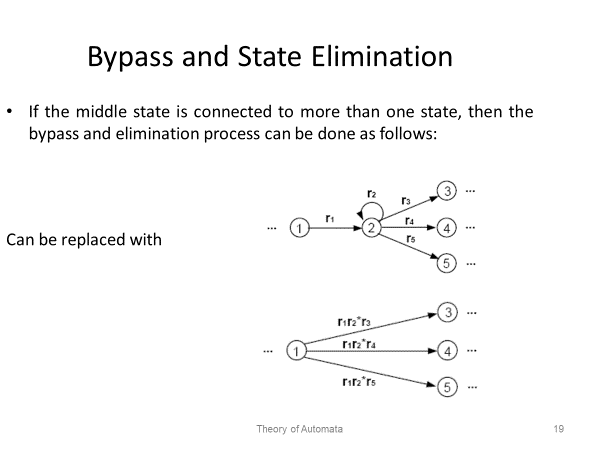
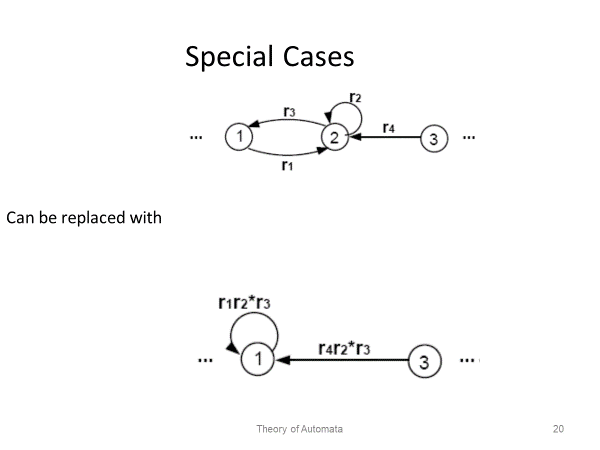
Automata theory has several real-world applications in a variety of domains since it deals with abstract machines and the issues they might resolve. Automata theory is important in the following domains: 

Computer Science and Programming Languages:
Automata play a crucial role in compiler design, particularly in lexical analysis. Token recognition in source code is achieved by using finite automata to implement patterns defined by regular expressions.
Verifying Syntax Pushdown automata and context-free grammars aid in the parsing and comprehension of programming language structure, ensuring that code follows proper syntax.

NLP, or natural language processing,

Text Parsing: To analyze and comprehend human language, finite state machines and probabilistic automata are employed in a variety of natural language processing (NLP) applications, including named entity recognition and part-of-speech tagging.

Speech Recognition: To describe sound sequences, speech recognition systems frequently employ Hidden Markov Models (HMMs), a kind of probabilistic automaton.

Network Protocols:
Protocol Verification: The use of automata theory facilitates the modeling and verification of communication systems and network protocols to make sure they function as intended under various circumstances.

Finite state machines can be used to model and analyze network traffic patterns, which can aid in performance monitoring and security.

Systems of Control:

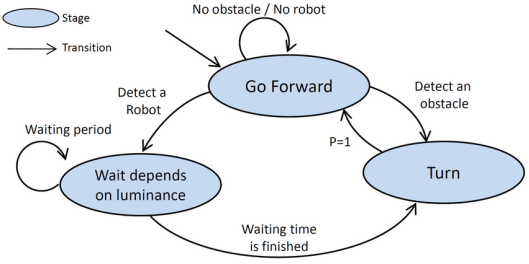
Automata are utilized in the design of control and embedded systems, including those seen in robotics and automation. Systems states and transitions can be modeled and controlled with the use of finite state machines.

Game Creation:

Behavior Modeling: Character and game element behavior is created and managed using automata models, such as finite state machines, to enable more dynamic and responsive interactions.

The field of bioinformatics

Sequence Analysis: In bioinformatics, automata are utilized for sequence alignment and analysis, including pattern recognition in protein structures or DNA sequences.

Design of Hardware:

Digital Circuit Design: To ensure that digital circuits and controllers function properly under a variety of circumstances, finite state machines are utilized in their design and implementation.

Robotics and Automation:

Path Planning: Finite state machines and other automata are used in robotics for path planning and obstacle avoidance. They help robots navigate complex environments by defining states for different stages of movement and decision-making.

Artificial Intelligence:

Behavior Trees: In AI, particularly in game AI, behavior trees use principles from automata theory to manage complex behaviors and decision-making processes in a structured way.

Data Compression:

Algorithm Design: Automata are used in algorithms for data compression. For example, the Lempel-Ziv-Welch (LZW) algorithm, which is used in file compression formats like GIF, relies on concepts from automata theory to efficiently encode data.

Text Search Algorithms:

Pattern Matching: Automata are fundamental to efficient text search algorithms. For instance, the Aho-Corasick algorithm uses a finite state machine to search for multiple patterns simultaneously in a text, making it highly efficient for applications like searching in large databases.

Cryptography:

Random Number Generation: Some cryptographic systems use automata to generate pseudorandom sequences of numbers. Linear feedback shift registers (LFSRs), which are a type of finite state machine, are commonly used in cryptographic applications for secure key generation and random number generation.

Context Free Grammar (CFG) Example

 Context-Free Grammar (CFGs) are a type of formal grammar used to describe languages in terms of production rules. CFGs are commonly used in computer science to define the syntax of programming languages, as well as in natural language processing for analyzing and generating sentences.

In this blog, we'll cover 10 basic examples of CFGs to help you better understand their structure and function.

1. Simplest CFG

The simplest CFG consists of a single production rule that generates the empty string:

S -> ε

This grammar generates only one string, which is the empty string.

2. Single-Character CFG

A CFG that generates a single character can be defined using the following production rule:

S -> a

This grammar generates only one string, which is the string "a".

3. Concatenation CFG

A CFG that generates strings by concatenating two smaller strings can be defined using the following production rule:

S -> AB

A -> a

B -> b

This grammar generates strings of the form "ab", where "a" and "b" are both single characters.

4. Alternation CFG

A CFG that generates strings by choosing between two different production rules can be defined using the following production rules:

S -> A | B

A -> a

B -> b

This grammar generates strings of the form "a" or "b", but not both.

5. Repetition CFG

A CFG that generates strings by repeating a single character can be defined using the following production rules:

S -> A

A -> aA | ε

This grammar generates strings of the form "a", "aa", "aaa", and so on.

6. Parentheses CFG

A CFG that generates strings with matching parentheses can be defined using the following production rules:

S -> (S)S | ε

This grammar generates strings with any number of matching parentheses, such as "()", "(())", and "((()))".

7. Palindrome CFG

A CFG that generates palindrome strings can be defined using the following production rules:

S -> ε | aSa | bSb

This grammar generates palindrome strings made up of the characters "a" and "b", such as "a", "aba", "abba", and so on.

8. Balanced Parentheses CFG

A CFG that generates strings with balanced parentheses can be defined using the following production rules:

S -> (S)S | ε

This grammar generates strings with any number of parentheses, as long as they are balanced, such as "()", "(())", "((()))", and so on.

9. Binary Numbers CFG

A CFG that generates binary numbers can be defined using the following production rules:

S -> 0S | 1S | ε

This grammar generates binary numbers made up of the digits "0" and "1", such as "0", "1", "10", "11", "100", and so on.

10. Arithmetic Expressions CFG

A CFG that generates arithmetic expressions can be defined using the following production rules:

S -> E

E -> E + T | E - T | T

T -> T * F | T / F | F

F -> (E) | num

This grammar generates arithmetic expressions made up of addition, subtraction, multiplication, and division, as well as parentheses and numerical values.

In conclusion, these 10 basic examples of CFGs demonstrate the flexibility and power of this formal grammar in generating a variety of different languages. By understanding the structure and function

Chomsky Normal Form (CNF) is a way to represent context-free grammars

 Chomsky Normal Form (CNF) is a way to represent context-free grammars in a specific form that makes it easier to analyze and manipulate the grammar. A grammar is in Chomsky's Normal Form if every rule has one of the following two forms:

A → BC, where A, B, and C are non-terminal symbols.

A → a, where A is a non-terminal symbol and a is a terminal symbol.

In other words, every rule must either produce two non-terminal symbols or a single terminal symbol. Additionally, the start symbol must only appear on the left-hand side of a rule, and there can be no rules that produce the empty string.

Converting a context-free grammar to Chomsky Normal Form can be a useful step in various algorithms for parsing and manipulating the grammar. The conversion process typically involves adding new non-terminal symbols and rules to the grammar, but the resulting grammar will have a simpler structure that is easier to analyze.

Kleene’s theorem with Proof

 

Video Lectures

Part1: https://youtu.be/MVrPfSgMxO8 

Part 2:    https://youtu.be/v296i02bZ6Q

Thus, to prove Kleene’s theorem, we need to prove 3 parts:

Part 1: Every language that can be defined by a finite automaton can also be defined by a transition graph.

Part 2: Every language that can be defined by a transition graph can also be defined by a regular expression.

Part 3: Every language that can be defined by a regular expression can also be defined by a finite automaton.

Proof of Part 1

 we know that every finite automaton is itself already a transition graph. Therefore, any language that has been defined by a finite automaton has already been defined by a transition graph.

Proof of Part 2: Turning TGs into Regular Expressions

We prove this part by providing a constructive algorithm:

– We present an algorithm that starts out with a transition graph and ends up with a regular expression that defines the same language.

– To be acceptable as a method of proof, the algorithm we present will satisfy two criteria: 

It works for every conceivable TG, and 

It guarantees to finish its job in a finite number of steps.

Algorithm 

Step 1: Create a unique, unenterable minus state and a unique, unleaveable plus state.

Step 2: One by one, in any order, bypass and eliminate all the non-minus or non-plus states in the TG. A state is bypassed by connecting each incoming edge with each outgoing edge. The label of each resultant edge is the concatenation of the label on the incoming edge with the label on the loop edge (if there is one) and the label on the outgoing edge.

Step 3: When two states are joined by more than one edge going in the same direction, unify them by adding their labels.

Step 4: Finally, when all that is left is one edge from - to +, the label on that edge is a regular expression that generates the same language as was recognized by the original TG.

OR Two Finite Automata FA3=FA1 OR FA1

 OR Two Finite Automata

Consider the following two FAs:

 

 

 

FA1 accepts all words with a double a in them.

FA2 accepts all words ending with b.

Let’s follow the algorithm to build FA3 that accepts the union of the two languages.

 

 

 

 

 

 

Transition Table

	Input	a	b
Step 1: State z1	z1=x1+y1	z2=x2+y1	z3=x1+y2
Step 2: State z2	z2=x2+y1	Z4=x3+y1	Z3=x1+y2
Step 3: State z3	z3=x1+y2	Z2=x2+y1	Z3=x1+y2
Step 4: State z4	z4=x3+y1	Z4=x3+y1	Z5=x3+y2
Step 5: State z5	z5=x3+y2	Z4=x3+y1	Z5=x3+y2

 

 

 

 

 

 

 

Step 1:

 

Step 1: State z1

z1=x1+y1

z2=x2+y1

z3=x1+y2

 

 

Step 2:

Step 2: State z2

Z=x2+y1

Z4=x3+y1

Z3=x1+y2

 

Step Final:

 

The Central Concepts of Automata Theory -Basic (Alphabet, Word and String )

 

What do automata mean?

Video

Lecture 

https://youtu.be/JMkXFcUl1Gg

It is the plural of automaton, and it means  “something that works automatically”

The word automata come from the Greek word αὐτόματος, which means "self-acting, self-computing, self-moving".

Theory of Automata

The theory of automata is a theoretical branch of computer science and mathematics. It is the study of abstract machines and the computation problems that can be solved using these machines.

The Central Concepts of  Automata Theory 

Alphabets

Strings

EMPTY STRING or NULL STRING: 

Words

All words are strings, but not all strings are words.

The Length of a String

It is often useful to classify strings by their length i.e. the number of position for symbol in the string.

For example 01101 has length 5.

It is common to say that the length of a string is “the number of symbols” in the string;

Substring