Kleene’s theorem with Proof

 

Video Lectures

Part1: https://youtu.be/MVrPfSgMxO8 

Part 2:    https://youtu.be/v296i02bZ6Q

Thus, to prove Kleene’s theorem, we need to prove 3 parts:

Part 1: Every language that can be defined by a finite automaton can also be defined by a transition graph.

Part 2: Every language that can be defined by a transition graph can also be defined by a regular expression.

Part 3: Every language that can be defined by a regular expression can also be defined by a finite automaton.

Proof of Part 1

 we know that every finite automaton is itself already a transition graph. Therefore, any language that has been defined by a finite automaton has already been defined by a transition graph.

Proof of Part 2: Turning TGs into Regular Expressions

We prove this part by providing a constructive algorithm:

– We present an algorithm that starts out with a transition graph and ends up with a regular expression that defines the same language.

– To be acceptable as a method of proof, the algorithm we present will satisfy two criteria: 

It works for every conceivable TG, and 

It guarantees to finish its job in a finite number of steps.

Algorithm 

Step 1: Create a unique, unenterable minus state and a unique, unleaveable plus state.

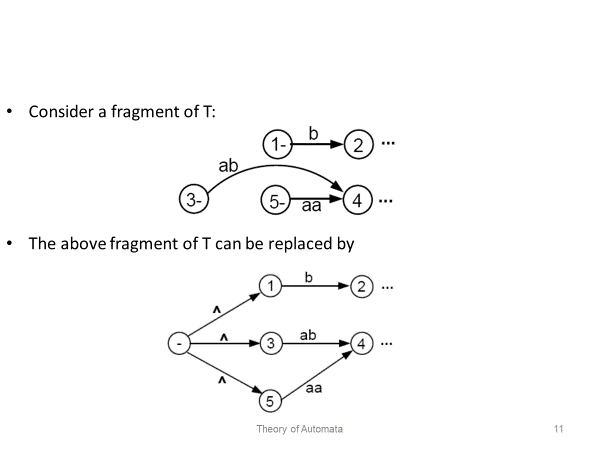
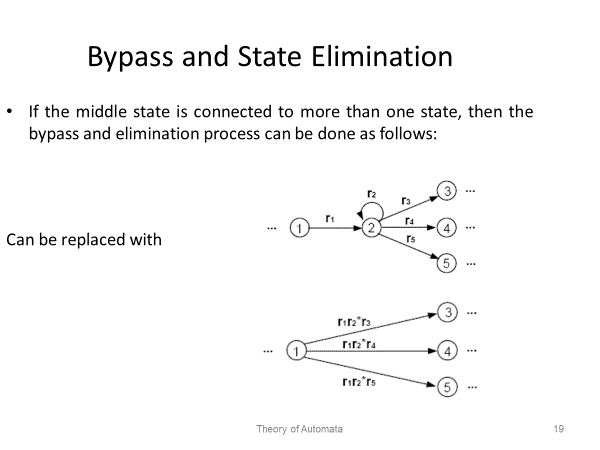
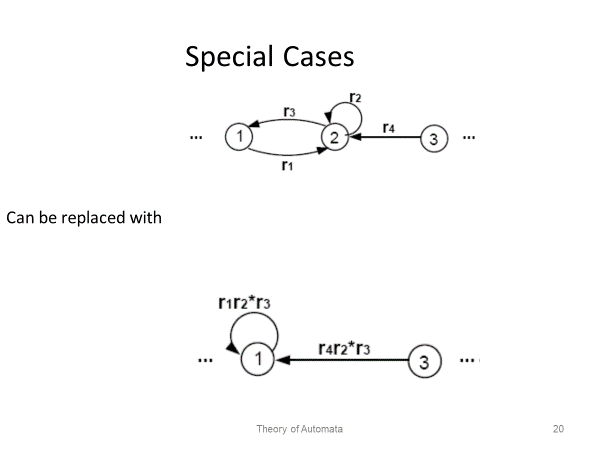
Step 2: One by one, in any order, bypass and eliminate all the non-minus or non-plus states in the TG. A state is bypassed by connecting each incoming edge with each outgoing edge. The label of each resultant edge is the concatenation of the label on the incoming edge with the label on the loop edge (if there is one) and the label on the outgoing edge.

Step 3: When two states are joined by more than one edge going in the same direction, unify them by adding their labels.

Step 4: Finally, when all that is left is one edge from - to +, the label on that edge is a regular expression that generates the same language as was recognized by the original TG.